The heat equation describes how heat flows in a material. In this example we look at a 2D region over which we solve initial value problems to describe heat flow. We obtain both symbolic and numerical results for our solutions.
Define the heat equation:
∂
t
u=
2
∇
u
in 2D:
In[2]:=
heat=D[u[x,y,t],t]==Laplacian[u[x,y,t],{x,y}]
Out[2]=
(0,0,1)
u
[x,y,t]
(0,2,0)
u
[x,y,t]+
(2,0,0)
u
[x,y,t]
Choose a region to solve the heat equation on:
In[6]:=
Graphics[Ω=Rectangle[{0,0},{2,1}]]
Out[6]=
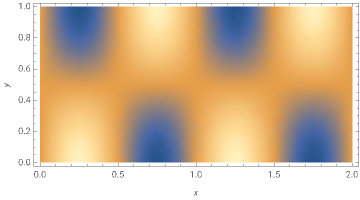
Select an initial condition for the heat of the region as an arbitrary function:
In[108]:=
ic=Sin[2πx]Cos[πy];DensityPlot[ic,{x,y}∈Ω,AspectRatioAutomatic,PlotLegendsAutomatic,FrameLabel{x,y}]
Out[108]=
Solve the heat equation on this region for the above initial conditions:
In[69]:=
sol[x_,y_,t_]=DSolveValue[{heat,u[x,y,0]==ic},u[x,y,t],{x,y,t}]
Out[69]=
-5
2
π
t

Cos[πy]Sin[2πx]
We see that the solution is just the same as the initial condition, but with a decaying exponential out front. This is because the initial condition could be separated into functions of each variable
u[x,y,0]=f[x]g[y]
with
f[x]=Sin[2πx]
and
g[y]=Cos[πy]
. What about an initial condition where this isn't true?
In[109]:=
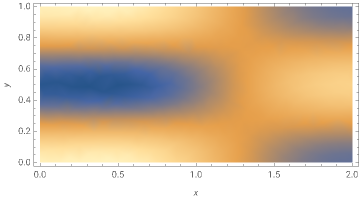
ic=Sin[πxCos[2πy]];DensityPlot[ic,{x,y}∈Ω,AspectRatioAutomatic,PlotLegendsAutomatic,FrameLabel{x,y}]
Out[109]=
Let's add a periodic boundary condition since our initial condition is periodic in
y
:
In[80]:=
BC=PeriodicBoundaryCondition[u[x,y,t],y==0,TranslationTransform[{0,1}]];
Solve the heat equation on Ω with this more complicated initial condition. This time use
NDSolveValue
to get a numerical result:
In[81]:=
sol[x_,y_,t_]=NDSolveValue[{heat,u[x,y,0]==ic,BC},u[x,y,t],{t,0,3},{x,y}∈Ω]
Out[81]=
InterpolatingFunction
Domain: {{0.,2.},{0.,1.},{0.,3.}}
Output: scalar
[x,y,t]
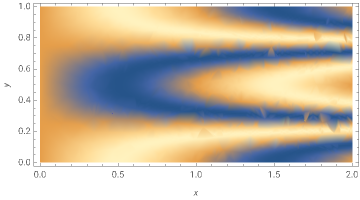
After just
t=0.1
, the higher frequency wiggles dissipated away and only the longer frequency wiggles survive:
In[110]:=
DensityPlot[sol[x,y,0.1],{x,y}∈Ω,AspectRatioAutomatic,FrameLabelAutomatic]
Out[110]=